Wavelet: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
== IDL code: SPEDAS == | == IDL code: SPEDAS == | ||
The SPEDAS IDL code uses Complex Morlet wavelets internally and computes the resulting power. | |||
<pre> | <pre> | ||
| Line 22: | Line 24: | ||
== Python code: pySPEDAS == | == Python code: pySPEDAS == | ||
Similar code in python uses the pywavelets library. This example uses the Complex Morlet wavelets. | |||
<pre> | <pre> | ||
| Line 39: | Line 43: | ||
pytplot.store_data(var, data={'x':time, 'y':y}) | pytplot.store_data(var, data={'x':time, 'y':y}) | ||
# Complex | # Complex Morlet wavelets transformation | ||
powervar = wavelet(var, | powervar = wavelet(var, wavename='cmorl0.5-1.0') | ||
pvar = powervar[0] | pvar = powervar[0] | ||
| Line 53: | Line 57: | ||
[[File:py_sin_wavelet.png|400px|||pyspedas spectrogram example]] | [[File:py_sin_wavelet.png|400px|||pyspedas spectrogram example]] | ||
With a small change, we can use a different wavelet, for example the Gaussian Derivative wavelet. | |||
<pre> | |||
import numpy as np | |||
import pytplot | |||
import pyspedas | |||
from pyspedas.analysis.wavelet import wavelet | |||
t = np.arange(4000.) | |||
y = np.sin(2*np.pi*t/32.) | |||
y2 = np.sin(2*np.pi*t/64.) | |||
y[1000:3000] = y2[1000:3000] | |||
var = 'sin_wav' | |||
time = pyspedas.time_float('2010-01-01') + 10*t | |||
pytplot.store_data(var, data={'x':time, 'y':y}) | |||
# Gaussian Derivative wavelets transformation | |||
powervar = wavelet(var, wavename='gaus1') | |||
pvar = powervar[0] | |||
pytplot.tplot_names() | |||
pytplot.options(pvar, 'colormap', 'jet') | |||
pytplot.ylim(pvar, 0.001, 0.1) | |||
pytplot.options(pvar, 'ylog', True) | |||
pytplot.options(pvar, 'ytitle', pvar) | |||
pytplot.tplot([var, pvar]) | |||
</pre> | |||
[[File:py_gaus1_wavelet.png|400px|||pyspedas spectrogram example]] | |||
Revision as of 17:48, 3 May 2020
Compare IDL code to python code for the wavelet transformation of a simple wave function.
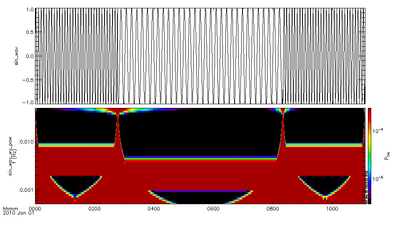
IDL code: SPEDAS
The SPEDAS IDL code uses Complex Morlet wavelets internally and computes the resulting power.
t = FINDGEN(4000)
time = time_double('2010-01-01') + 10*t
data = sin(2*!pi*t/32.)
data2 = sin(2*!pi*t/64.)
data[1000:3000] = data2[1000:3000]
var = 'sin_wav'
store_data, var, data={x:time, y:data}
pvar = 'sin_wav_wv_pow'
wav_data, var
tplot, [var, pvar]
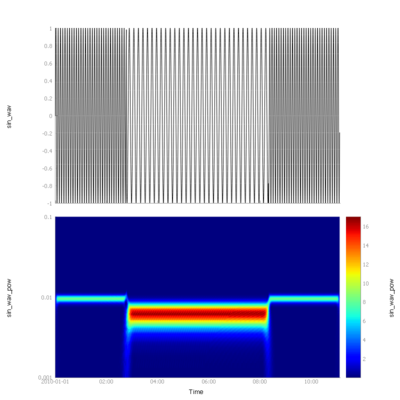
Python code: pySPEDAS
Similar code in python uses the pywavelets library. This example uses the Complex Morlet wavelets.
import numpy as np
import pytplot
import pyspedas
from pyspedas.analysis.wavelet import wavelet
t = np.arange(4000.)
y = np.sin(2*np.pi*t/32.)
y2 = np.sin(2*np.pi*t/64.)
y[1000:3000] = y2[1000:3000]
var = 'sin_wav'
time = pyspedas.time_float('2010-01-01') + 10*t
pytplot.store_data(var, data={'x':time, 'y':y})
# Complex Morlet wavelets transformation
powervar = wavelet(var, wavename='cmorl0.5-1.0')
pvar = powervar[0]
pytplot.tplot_names()
pytplot.options(pvar, 'colormap', 'jet')
pytplot.ylim(pvar, 0.001, 0.1)
pytplot.options(pvar, 'ylog', True)
pytplot.options(pvar, 'ytitle', pvar)
pytplot.tplot([var, pvar])
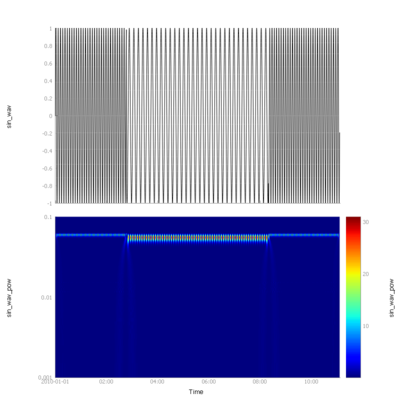
With a small change, we can use a different wavelet, for example the Gaussian Derivative wavelet.
import numpy as np
import pytplot
import pyspedas
from pyspedas.analysis.wavelet import wavelet
t = np.arange(4000.)
y = np.sin(2*np.pi*t/32.)
y2 = np.sin(2*np.pi*t/64.)
y[1000:3000] = y2[1000:3000]
var = 'sin_wav'
time = pyspedas.time_float('2010-01-01') + 10*t
pytplot.store_data(var, data={'x':time, 'y':y})
# Gaussian Derivative wavelets transformation
powervar = wavelet(var, wavename='gaus1')
pvar = powervar[0]
pytplot.tplot_names()
pytplot.options(pvar, 'colormap', 'jet')
pytplot.ylim(pvar, 0.001, 0.1)
pytplot.options(pvar, 'ylog', True)
pytplot.options(pvar, 'ytitle', pvar)
pytplot.tplot([var, pvar])